ここに記載の用途以外にも使われることがあります。
アルファベットの用途は慣例を含めればかなり広いので、ある程度範囲を絞って載せていきます。
種類が多いので、目次をうまく活用してください。
※現在更新中!個別の記事ができたらリンクも付ける予定です。
$a$
主に定数や係数として用いられる文字。
特別な性質がない場合にはまず使われると考えて良い。
アルファベットの最初の文字なので、使用頻度も多い。
また、「加速度$a$(acceleration)」などの意味を持たせて使うこともある。
$A$
主に集合や行列として用いられる文字。
アルファベットの最初の文字なので、使用頻度も多い。
集合や行列で例示する時によく使われる。
abc予想
$a+b=c$ を満たす、互いに素な自然数の組 ( $a$, $b$, $c$ ) に対し、積 $abc$ の互いに異なる素因数の積を $d$ と表す。このとき、任意の ε > 0 に対して、
$$c > d^{1+ε}$$
を満たす組 ( $a$, $b$, $c$ ) は高々有限個しか存在しない。
$d$ は $abc$ の根基 (こんき、radical)といい、rad$( abc )$ と書く。
1985年にジョゼフ・オステルレとデイヴィッド・マッサーにより提起された数論の未解決予想。
自然数 $abc$ の足し算と掛け算の関係について予想をしている。
2012年、京都大学数理解析研究所の望月新一教授による、証明の論文がインターネットに公表され、約8年後には数学誌にも掲載(査読を通過したので、正しいだろうと認められた)となったのだが、現在も本当に証明が正しいのかどうか懐疑的な見解がある。
arc- (Arc-)
逆三角関数(三角関数の逆関数)で用いられる接頭辞。
例えば、tan$x$には「arctan$x$」のように三角関数の頭に付ける。
arcは弧を意味し、「アーク」と読む。逆三角関数の値がラジアン(単位円の円弧の長さ)であることから由来する。
「arctan$x$」は「Tan$^{-1}x$」のようにー1を添えた表記もあるが、逆数と混同しやすい(逆数とは別物である)ために、頭文字を大文字にするなどの差別化がされることがある。
arg z (Arg z)
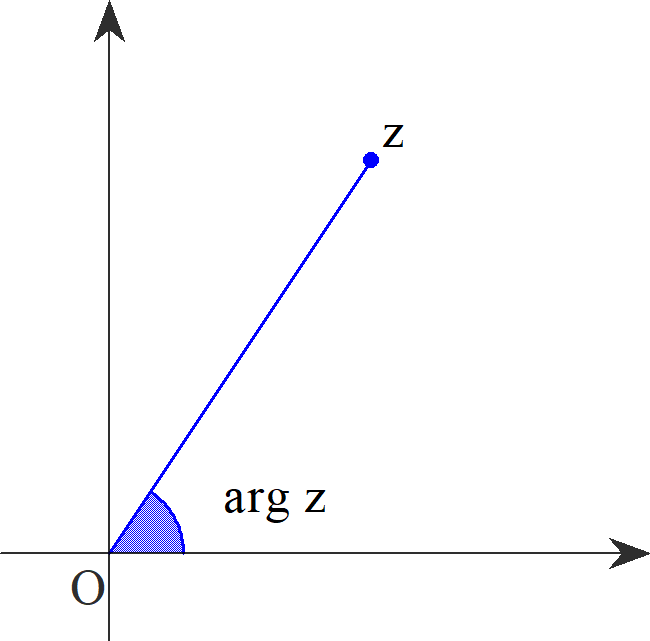
複素数平面における、複素数の偏角(argument of complex)のこと。zは複素数を表している。
argは「アーギュ」または「アーグ」と読む。
偏角は正の実軸から動径Ozまでを測った角度である。複素数を極形式で表す際に使用される。
$b$
主に定数や係数として用いられる文字。
用途は$a$と同じだが、「$a$の次」、「2番目」という性質が強い。
文字が2つ以上用いられるときは、$a$とセットでよく使われる。
$B$
主に集合や行列として用いられる文字。
用途は$A$と同じだが、$A$をすでに使用している場合、2つ目の集合や行列として用いられる。
集合では、2つ以上の集合の関係を表すことが多いため、使用頻度は高い。
$c$
主に定数や係数として用いられる文字。
「$b$の次」、「3番目」という性質が強い。
文字が3つ以上用いられるときは、$a$や$b$とセットでよく使われる。
$C$
① 集合や行列として用いられる。「$A$、$B$に次ぐ3つ目」として使い、使用頻度も比較的高い。
② 「複素数全体(complex number)」を表す集合として使用する。太字や中抜き文字で表すことが多い。
③ 積分定数として用いられる文字。不定積分をした際に、定数部分を表すために使う。
定数は英語で「constant」であるから、$C$を使うとされている。
④ 組合せの総数(combination)の計算に用いられる文字。${}_n \mathrm{C}_r$のように表記する。
cos
三角関数の一つ。cosine(コサイン)、余弦(よげん)と呼ぶ。
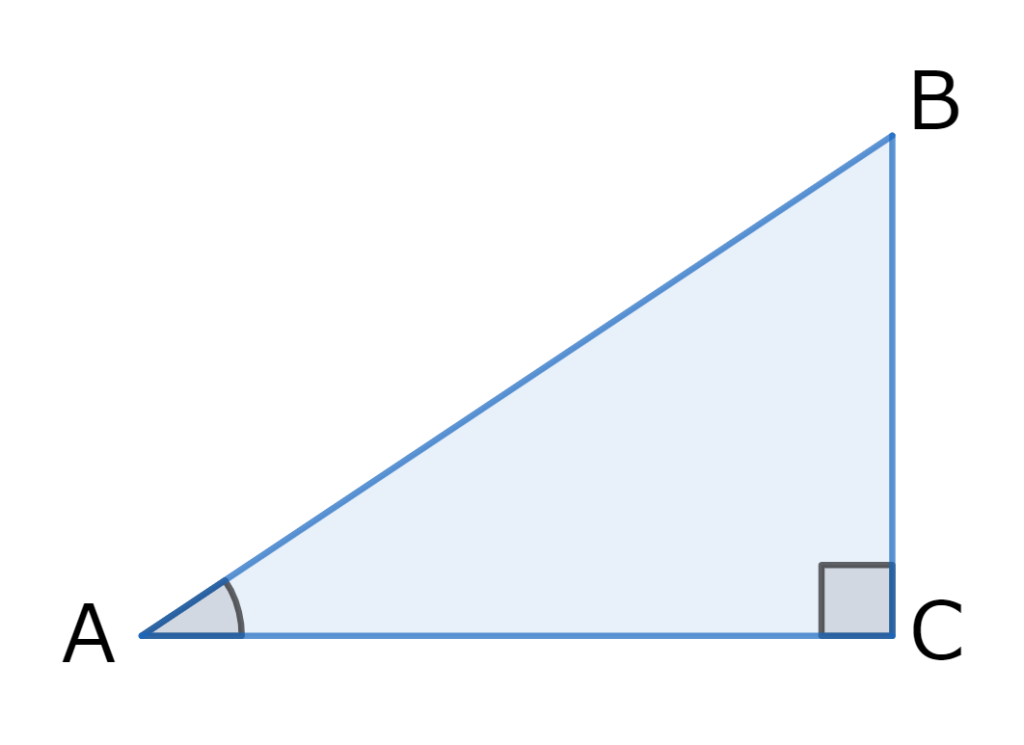
図の三角形ABCの角Aに対して、
$$\cos A = \frac{AC}{AB} $$
と定義できる。(三角比)
単位円により拡張すると、一般角の範囲で扱うことができる。
角Aの正弦(sine・サイン)に対し、余角(直角三角形のもう一つの鋭角)、つまり角Bの正弦によって表せるため、余弦(余角の正弦、complementary angles sine)と呼ばれている。
cot
三角関数の一つ。cotangent(コタンジェント)、余接(よせつ)と呼ぶ。
図の三角形ABCの角Aに対して、
$$\cot A = \frac{AC}{BC} $$
と定義できる。(三角比)
単位円により拡張すると、一般角の範囲で扱うことができる。
角Aの正接(tangent・タンジェント)に対し、余角(直角三角形のもう一つの鋭角)、つまり角Bの正接によって表せるため、余接(余角の正接、complementary angles tangent)と呼ばれている。

csc (cosec)
三角関数の一つ。cosecant(コセカント)、余割(よかつ)と呼ぶ。
略しないでcosecと書くこともある。(略さない方が主流)
図の三角形ABCの角Aに対して、
$$\csc A = \frac{AB}{BC} $$
と定義できる。(三角比)
単位円により拡張すると、一般角の範囲で扱うことができる。
角Aの正割(secant・セカント)に対し、余角(直角三角形のもう一つの鋭角)、つまり角Bの正割によって表せるため、余割(余角の正割、complementary angles secant)と呼ばれている。

$d$
① 「$c$の次」、「4番目」という性質をもつ定数、係数。使用頻度は低め。
② 「距離(distance)」を表す文字として使用する。主に「2点間の距離」で用いられる。
$$ d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}} $$
③ 「約数(divisor)」を表す文字として使用する。約数関数の式を表す際に用いる。
④ 微分で表記される「無限小の変化量」のこと。例えば、$dx$ は極めて小さく変化した $x$ のこと。
導関数はその定義により、以下のように表記できる。ライプニッツの記法という。
$$\frac{dy}{dx}$$
$D$
① 集合や行列として用いられる。「$A$、$B$、$C$に次ぐ4つ目」として使う。
② 判別式を表す文字として使用する。discriminantの頭文字。$Δ$を使うこともある。
2次方程式の解に対する判別式で使用することが多い。$D=b^2-4ac$
$e$
① ネイピア数。自然対数の底ともいう。超越数であり、主に極限や微積分において重要な性質を持つ。
2.71828182845904…
② 単位ベクトルで用いられる文字。 $\vec{e}$ か $e$ の太字で表記する。ドイツ語のEinheitsvektorに由来。
$E$
① 単位行列。正方行列であり、対角成分にすべて1が並び、他はすべて0になっている。
② 確率変数の期待値として用いる文字。確率分布に対しては平均と呼ぶことがある。
$f$
関数や写像(function)を表す。$x$ の関数として $f(x)$ と書くことが多い。
大文字を使って $F(x)$ とすることがあるが、「$f(x)$ の原始関数」などのように、$f(x)$ との関係性が強いものに対して使うことが多い。
$F$
① 代数学における可換体(field)を表す文字として使われる。ただし、$K$(ドイツ語でKörper)を使うことの方が多い。
② 関数や写像(function)を表す文字。 $f$ が使われている場合、何らかの関係性を持っている。
③ 論理学における偽(false)の意味で用いる。真は $T$ (true)である。
$g$
① 図形の重心(center of gravity)。三角形の重心は、図形問題で頻出。
② 関数や写像を表す文字。 $f$ に次いで用いられ、$g(x)$ のように表記する。使用頻度は高い。
$G$
① 図形の重心(center of gravity)。図形で点を表記するときは、こちらの大文字を使う。
② 群(group)を表す文字として使われる。群は代数的構造の集合である。
③ 関数や写像を表す文字。 $F$ に次いで用いる。
関数の $g$ が使われている場合、何らかの関係性を持っている。
$h$
① 図形における高さ(height)。三角形の高さを文字で表すときなどに用いることが多い。
② 平均変化率や極限の式に用いられる文字。微小の変化量、幅として考える。
なぜ $h$ を用いるのかは分かっていないが、古くからの慣例である。以下の式は微分の定義。
$$\lim_{h \rightarrow 0}\frac{f(x+h)-f(x)}{h}$$
$H$
$i$
① 虚数単位(imaginary unit)。「$i^2=-1$」と定義され、複素数において重要な役割を担う。
② 添字(同じ文字を区別するために、文字に小さく添えるもの、index)として$j$、$k$とともに使用される。
例えば、行列の成分では $a_{ij}$ と表記し、$i$ が行番号、$j$ が列番号を表している。
$I$
① 積分(integral calculus)の置き換えをするときに用いられることが多い。
部分積分を行うと、「元と同じ式が出てくる」という場合などに有効な方法である。
② 区間(interval)を表す文字。$x$ の定義域がその一例。区間は集合として考える。
実数範囲では、数の大小関係が成り立つため、区間は実数の集合として見ることができる。
$j$
基本的には「 $i$ の次」という意味で用いる。用途も $i$ と同じ。
① 虚数単位。数学ではなく電気工学の分野で、電流の $i$ と区別するために使う。
② 添字(同じ文字を区別するために、文字に小さく添えるもの)として$i$、$k$とともに使用される。
例えば、行列の成分では $a_{ij}$ と表記し、$i$ が行番号、$j$ が列番号を表している。
$J$
$k$
① 定数として使う。定数はドイツ語で「Konstante」であることから、優先的に使うことも多い。
② 添字(同じ文字を区別するために、文字に小さく添えるもの)として$i$、$j$とともに使用される。
$K$
① 代数学における可換体(ドイツ語でKörper )を表す文字として使われる。
② 運動エネルギー(kinetic energy)を表す文字。
$l$
① 長さ(length)を表す文字。図形問題だけではなく、関数の分野にも使用される。
② 主に自然数や整数を表す定数として、 $n$ 、 $m$ に次ぐ3番目として使用される。
$L$
lim
極限(limit)として用いられる記号。リミットと読む。以下のように扱う。
$$\lim_{n \rightarrow 0}\frac{1}{n}$$
例えば、この式のlimは「$n$を限りなく0に近づける」ことを表している。
実際には $n=0$ とはならず、「近付いていく先の値」と考える。
$m$
① 主に自然数、整数を表す定数として、$n$ に次ぐ2番目として使用される。
② 質量(mass)を表す。主に物理で使用する。
③ 最小値(min)として、1文字で使用する。最大値(max)と区別するため、小文字で表す。
$M$
① 最大値(max)として、1文字で使用する。最小値(min)と区別するため、大文字で表す。
② $N$ に次いで、集合、行列や、とても大きい数を表す文字として使用する。
max
最大値(maximum)のこと。マックスと読む。最初を大文字にしてMaxとすることもある。
与えられた範囲内でとる最も大きい値。
極大値でも同じつづり(maximal value)であるが、極値として使用することはほとんどない。
min
最小値(minimum)のこと。ミニマムと読むが、つづりから、ミンと読むこともある。
与えられた範囲内でとる最も小さい値。
極小値でも同じ綴り(minimal value)であるが、極値として使用することはほとんどない。
mod ( modulo )
「法(割る数)として」という意味をもつ、合同式で用いられる文字。
元は「modulo(モジュロ、測定の意味)」だが、慣例で「mod」と書き、「モッド」と読む。
整数の合同について述べたもので、図形の合同とは意味が異なる。以下は定義である。
2つの整数 $a$ 、 $b$ を自然数 $n$ で割った余りが等しいとき、
$$ a ≡ b ( \mathrm{mod} n )$$と表し、 $a$ と $b$ は $n$ を法として合同であるという。
高校では発展的な内容という扱いで習わない学校も多いが、整数問題で非常に使える式であるため、学習塾で取り扱われて学んだり、独学で学んだりする人も多い。
$n$
① 自然数(natural number)を表す文字。使用頻度は非常に高い。
証明等においても、自然数を扱う場合は、まず $n$ を使う。
自然数を用いた数列や添字としてもよく使われ、「1番目、2番目、3番目、…、$n$ 番目、…」のように扱う。
② 整数を表す定数や係数として使用する。$n$ 自体は自然数としての意味合いが強い。
$N$
① 「自然数全体(Natural number)」を表す集合として使用する。太字や中抜き文字で表すことが多い。
② 非常に大きな自然数、または整数として扱う。
$o$
数字の0と紛らわしいため、定数としてはほとんど使用されない文字。
ゆえに、自然数は $n$ → $m$ → $l$ というように使う順番はアルファベット順の逆をたどる。
あえて、0と同じ意味で用いることもある。
① 原点(origin)として用いる文字。0の代わりとして使われることもある。
どちらかといえば、大文字にして使うことが多い。
② 位数。集合に入っている元の個数(濃度)。基本的には「ord」と表記する。
$O$
① 原点(origin)として用いる文字。 円の中心として表記することもある。
② 零行列。成分がすべて0の行列。
③ 零元。広い意味での数字の0と考えて良い。零行列も零元の一つ。
$p$
① 点(point)を表す文字。図形における点は、$p$ → $q$ → $r$ →…の順に使用する。
② 素数(prime number)を表す文字。整数の分野で頻繁に使用される。
③ 主に有理数や実数を表す定数。文中で「実数 $p$ とする」などと限定してから使用する場合が多い。
④ 命題(proposition)、特に条件命題「$ p ⇒ q $」で使用される。
$p$ 自体を命題として使うこともある。
$P$
① 「素数全体(prime number)」を表す集合として使用する。太字や中抜き文字で表すことが多い。
② 順列(permutation)の計算に用いられる文字。${}_n \mathrm{P}_r$のように表記する。
③ 確率(possibility)として用いる文字。$P(A)$ は「事象 $A$ の確率」を表す。
④ 多項式(polynominal)として置く文字。主に $x$ の式であることから、$P(x)$ と表記する。
⑤ 命題(proposition)を表す集合として用いる。
$q$
基本的に $p$ に次いで使用するため、用途は $p$ とほぼ同じ。
① 点、素数、定数、命題を表す文字。詳細は $p$ にて。基本的に$p$ の次に使用する。
② 商(quotient)として使用される文字。割り算をするとき、割る数として使用することが多い。
$Q$
① 「有理数全体(quotient、商の意味)」を表す集合として使用する。太字や中抜き文字で表すことが多い。
有理数はrational numberというが、実数のreal numberと頭文字が重複するため、$Q$ を使う。
② 商(quotient)として置く文字。 主に $x$ の式であることから、$Q(x)$ と表記する。
③ 集合等で $P$ に次いで用いる文字。
q.e.d. (Q.E.D.)
議論や証明を終えて、結論を述べた後に付ける記述。証明終了の意味で使う人も多いが、厳密な意味は後述する。
数学でも使われることがあり、証明の最後に「Q.E.D.」と書く。
ラテン語で「Quod Erat Demonstrandum」といい、決して「Question End」の略ではないので注意したい。
意味は「以上が証明されるべき事柄であった」。
実は「証明終了」の意味は持たないため、「よって、~である」と結論を述べてから使う必要がある。
$r$
① 円の半径(radius)として使う文字。特に内接円では小文字が使用される。
② 主に実数を表す定数。実数全体の要素として使うことが多い。
$R$
① 「実数全体(real number)」を表す集合として使用する。太字や中抜き文字で表すことが多い。
② 円の半径(radius)として使う文字。特に外接円では大文字が使用される。
③ 環(ring)を表す文字。最も簡単な例は、整数全体の集合に加法と乗法をつけたものである。
$s$
① 面積(surface、sum)を表す文字。大文字を使うことも多い。
② 和(sum)を表す文字。主に無限級数にて用いられる。
③ 定数やパラメータとして、$r$ や $t$ に次ぐ2番目として使うことが多い。
④ データにおける標準偏差(standard deviation)を表す文字。この場合、 $s^2$ は分散を指す。
$S$
① 面積(surface、sum)を表す文字。
② 集合等で、$R$ や $T$ に次ぐ2番目として使うことが多い。
sec
三角関数の一つ。secant(セカント)、正割(せいかつ)と呼ぶ。
図の三角形ABCの角Aに対して、
$$\sec A = \frac{AB}{AC} $$
と定義できる。(三角比)
単位円により拡張すると、一般角の範囲で扱うことができる。
sin、cos、tanの3つに比べて、使用する機会はほぼない。
しかし、海外ではsec、cosec、cotの3つを中心に学んでいる国もある。

sin
三角関数の一つ。sine(サイン)、正弦(せいげん)と呼ぶ。
図の三角形ABCの角Aに対して、
$$\sin A = \frac{BC}{AB} $$
と定義できる。(三角比)
単位円により拡張すると、一般角の範囲で扱うことができる。
三角関数はsin、cos、tanの3つを主に使う。
特にsinとcosは非常に幅広い分野で使用される。

s.t.
such thatの略。「~のような」の意味。
主に、記号∃(「存在する」の意)とセットで以下のように使う。
$$∃x ∈ \mathbb{N} s.t. f(x)=1$$意味は、「$f(x)=1$ となるような自然数 $x$ が存在する」となる。
$t$
① 時間(time)を表す文字。時間の経過を表す変数としても使用される。
② 媒介変数(パラメータ)として使う。
元々は物理における物体の位置に対し、 時間(time)の要素を考えたため、$t$ を使用するとされている。
$T$
① 時間(time)を表す文字。小文字 $t$ と違い、定数(固定された時間)としての意味がある。
② 転置行列の添字。 $A^T$ のように表記する。元の $A$ とは行と列を入れ替えた行列となる。
③ 論理学における真(true)の意味で用いる。偽は $F$ (false)である。
tan
三角関数の一つ。tangent(タンジェント)、正接(せいせつ)と呼ぶ。
図の三角形ABCの角Aに対して、
$$\tan A = \frac{BC}{AC} $$
と定義できる。(三角比)
単位円により拡張すると、一般角の範囲で扱うことができる。
三角関数はsin、cos、tanの3つを主に使う。
tanはその定義から、直線の傾きを表すために使われることがある。

$u$
① 定数や変数として使用する文字。$v$ の次として扱う場面が多い。
微分積分や物理学に関わる分野で使用される。
② 関数として扱う文字。主に合成関数の微分の定義で見ることになる。
③ ベクトル変数として、$v$ の次に使用される。
$U$
① 集合の中で、特に全体集合(Universal Set)として用いられる。
② ユニタリ(unitary、単一、単位の)の性質を持つものに使われる。代数学で主に使われる。
$v$
① ベクトル(vector)変数で使用される。矢印のない $v$ 自体がベクトルを表すこともある。
② 速度(velocity)として使用される。特に、物理にて速度の変数として使われる。
$V$
① ベクトル(vector)空間で使用される。
② 統計学における分散を表す。特に確率変数における分散を指す。
$w$
① $x$ 、 $y$ 、 $z$ に次ぐ第4の未知数。使用頻度は低め。
② 複素数変数として、$z$ に次ぐ2番目に使用する。複素数のωと似ているが別物なので注意。
③ 科学において、 $v$ の代わりに使用することがある。
$W$
① $X$ 、 $Y$ 、 $Z$ に次ぐ第4の未知の集合、行列。
② 仕事(work)の計算で用いる。物理、化学の仕事のほか、仕事算の計算例にも使うことがある。
$x$
① 未知数として扱う文字。 値が確定していない、あるいはわからない変数である。
17世紀のフランスの哲学者・数学者のデカルトが使い始めたものとされる。
② 座標軸の1つ。$x$ 軸。座標空間を表すために重要な役割を果たす。
複素数平面では実軸の役割を持つ。
$X$
① 未知である集合や空間、行列に付けられる文字。
② 不定元として用いられる文字。小文字 $x$ と用途は似ており、多項式や形式的級数にて使用される。
$y$
① $x$ に次ぐ第2の未知数。使用頻度は非常に高い。
② 座標軸の一つ。 $y$ 軸。平面では上下、3次元空間では奥行を表す。
複素数平面では虚軸の役割を持つ。
$Y$
① 未知である集合や空間、行列に付けられる文字で、$X$ に次ぐ第2の文字として使う。
② 不定元として用いられる文字。$X$ と用途は同じである。
$z$
① $x$ 、 $y$ に次ぐ第3の未知数。$x$ 、 $y$ 比べると使用場面はかなり限定的。
② 複素数変数(ドイツ語のKomplexen Zahlen)として使用する。
実数における変数 $x$ と同じ役割である。
③ 座標軸の一つ。 $z$ 軸。3次以上の空間を表すために使われる。
$Z$
① 集合として用いられる。「$X$、$Y$に次ぐ3つ目」として使うことが多い。
② 「整数全体(Zahlen※ドイツ語で「数」)」を表す集合として使用する。太字や中抜き文字で表すことが多い。