種類が多いので、目次をうまく活用してください。
中高数学を中心にまとめます。大学数学の用語は今のところ優先順位が低いのでご了承ください。
※現在更新中!個別の記事ができたらリンクも付ける予定です。
解【かい】
方程式を成り立たせる未知数の値のこと。主に方程式において、未知数 $x$ に当てはまる数値のこと。
$$x-3=2$$例えば上記の式においては、 $x$ に $5$ を当てまめることで、
$$5-3=2$$という正しい等式が成立する。この場合、「$5$」が解ということになる。
様々な方程式が存在し、その解を求める方法は多岐にわたる。
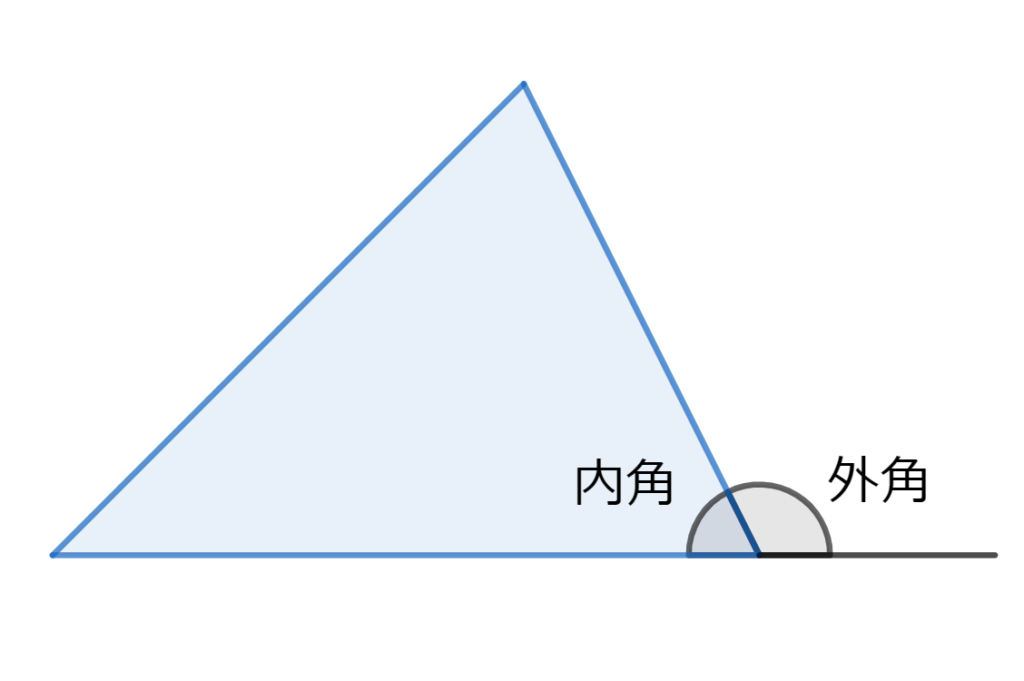
外角【がいかく】
多角形で、1つの辺とその隣の辺の延長線がつくる角。平面図形の外側にできる角で、図形の内側の角(内角)に隣り合っている。
外角には主に以下の性質がある。
・多角形の外角の和は$360°$
・三角形の外角は、隣り合わない2つの内角の和と等しい(外角の定理)
階級【かいきゅう】
統計の「度数分布」で用いられるデータの区間のこと。
例えば、身長のデータをまとめる際、「140cm以上150cm未満」「150cm以上160cm未満」というように一定の数値で区切りながらまとめていくことがある。この「140cm以上150cm未満」のような区間が階級である。
データを分析するときには、階級の幅をどのように設定するのかが重要とされる。
階級値【かいきゅうち】
統計における階級の中央の値。
例えば、「140cm以上150cm未満」という階級であれば、階級値は「145cm」である。
「140cm以上150cm未満」の度数(人数)が50であれば、「約145cmの人が50人いる」と概算ができるため、数値がバラバラかつ個数が多いデータの大まかな平均値をとるために役立つ。
開区間【かいくかん】
両端点を含まない区間のこと。
主に、集合 {$x|a<x<b$} と表す。また、$(a,b)$とも表記する。
例えば、 $2<x<5$ であれば、「2より大きく、5より小さい」という開区間を表すことになり、この区間には「2」と「5」は入らない。
括弧を使った$(a,b)$のような表記は、座標や最大公約数などでも使用されるが、明確に区別する書き方もないため、文脈で読み取ることになる。

階差数列【かいさすうれつ】
ある数列に対し、各項の差をとることで表れる数列のこと。
例えば、
$$1,2,4,7,11,16,22,…$$という数列で、前後の数字の差をとると、
$$1,2,3,4,5,6,…$$という数列を作ることができる。これが階差数列である。
等差、等比数列のどちらでもないとき、階差数列をつくることで法則性を見つけられる場合が多い。
階乗【かいじょう】
正の整数 $n$ に対し、1から $n$ までのすべての整数の積のこと。$n!$ と表す。
$n$ 個の異なるものを1列に並べるときの総数であるが、様々な場面で登場する計算である。
ちなみに、「0!=1」と定義される。実際、値を1と定義したほうが都合の良い場面が多い。
基本的には正の整数で考えられる計算だが、ガンマ関数(解析学)を用いることで、整数でない数値の階乗も定義できるようになる。
外心【がいしん】
三角形の各辺の垂直二等分線の交点のこと。外接円の中心。
概数【がいすう】
外積【がいせき】
解析/解析学【かいせき/かいせきがく】
外接【がいせつ】
回転【かいてん】
回転体【かいてんたい】
解の公式【かいのこうしき】
外分【がいぶん】
ガウス【がうす】
19世紀の数学者、ヨハン・カール・フリードリヒ・ガウスのこと。
近代数学に与えた影響は大きく、ガウスの名を持つ法則などが多く存在する。
ガウスには有名な逸話があり、
“7歳の時、算数の授業で教師が「1から100までの数字すべてを足せ」という問題を出し、生徒たちが問題を解くには相当な時間がかかるだろうと考えていたが、ガウスはわずか数秒で「5050」という解答を出し、教師を驚かせた。“
というものである。
これは「$1+100=101$、$2+99=101$…」というように101のかたまりを50個つくるという「等差数列の和」の考え方を7歳で発見したというものである。
創作ではないかという説もあるが、幼いときから非凡な才能があったことは間違いなく、この話を始めとする様々な逸話が生まれてくることこそが、その才能の裏付けをしていると考えられる。
ガウス記号【がうすきごう】
可換【かかん】
角【かく】
確率【かくりつ】
確率分布【かくりつぶんぷ】
確率変数【かくりつへんすう】
加減乗除【かげんじょうじょ】
加減法【かげんほう】
過剰数【かじょうすう】
傾き【かたむき】
下端【かたん】
加法【かほう】
関数/函数【かんすう】
完全数【かんぜんすう】
幾何/幾何学【きか/きかがく】
奇関数【きかんすう】
貴金属比【ききんぞくひ】
基数【きすう】
奇数【きすう】
軌跡【きせき】
期待値【きたいち】
帰納法【きのうほう】
逆【ぎゃく】
逆関数【ぎゃくかんすう】
逆算【ぎゃくさん】
逆数【ぎゃくすう】
既約分数【きやくぶんすう】
球【きゅう】
級数【きゅうすう】
求積法【きゅうせきほう】
境界線【きょうかいせん】
狭義【きょうぎ】
共通部分【きょうつうぶぶん】
共分散【きょうぶんさん】
共役【きょうやく】
共有点【きょうゆうてん】
行列【ぎょうれつ】
行列式【ぎょうれつしき】
極限【きょくげん】
極限値【きょくげんち】
曲線【きょくせん】
極値(極大値・極小値)【きょくち(きょくだいち・きょくしょうち)】
虚数【きょすう】
距離【きょり】
切り上げ【きりあげ】
切り捨て【きりすて】
近似【きんじ】
近似値【きんじち】
空間【くうかん】
空間座標【くうかんざひょう】
偶関数【ぐうかんすう】
空集合【くうしゅうごう】
偶数【ぐうすう】
区間【くかん】
数直線上のある2点とその間にある範囲を表した集合のこと。
言葉で具体例を挙げるならば、「100以上1000未満」といった表現も区間の一つとなる。
基本的には実数の集合であるが、整数などの「全順序集合」であれば区間は作れる。
区間の両端点を含むか含まないかで表現が異なる。
両端点を含むときは「閉区間」、含まないときは「開区間」、片方だけ含まないときは「半開区間」という。