種類が多いので、目次をうまく活用してください。
中高数学を中心にまとめます。大学数学の用語は今のところ優先順位が低いのでご了承ください。
※現在更新中!個別の記事ができたらリンクも付ける予定です。
値【あたい】
数の大きさ。文字が表す数字のこと。数値ともいう。
「最大値」のように、その数字の特徴を表す言葉と一緒に使うことも多い。
余り【あまり】
割り算で割り切れずに残った数のこと。
例えば、8個のものを3個ずつに分けるという「$8÷3$」の計算をしたとき、
(●●●)(●●●) ●●
上記の●2個のように、きれいに分けられずに残ってしまうものがある。これを「余り2」とする。
アラビア数字【あらびあすうじ】
日常的に用いる数字「0,1,2,3,4,5,6,7,8,9」のこと。
起源はインドだが、アラビア経由でヨーロッパに広まったため、アラビア数字と呼ぶ。
計算するときに用いる数字のため、算用数字とも呼ぶ。
他の数字の種類は、ローマ数字(Ⅰ、Ⅱ、Ⅲ、Ⅳ、・・・)などがある。
暗算【あんざん】
計算の流れを物を使ったり、紙に書いたりしないで、頭の中だけで計算すること。
1桁の数字の四則(+-×÷)や「繰り上がり・繰り下がり」のない計算は小学校の早い段階で習得することになる。
複雑な計算はある程度の訓練を要する。特に、繰り上がりや繰り下がりをうまく処理できるかが課題。
算数や数学で「一番身に付けると役に立つ力」と聞かれたら、これを挙げる人がほとんどかもしれない。
以下【いか】
数の大小関係や範囲を表し、その数自身を含み、それを下回る範囲のこと。
例えば、「5以下の自然数」と聞かれたら、「1,2,3,4,5」のように、5も含めて答える。
不等式で表すときには、≦や≧を使う。 例、$x$は5以下の数 → $x≦5$
似た言葉で「未満」があるが、その数自身を含まないという違いがある。
移項【いこう】
等式または不等式で、一方の辺にある項を、符号を変えて他の辺に移すこと。
両辺に同じ数を加えたり減らしたりしても成立するという性質を利用したもの。
以上【いじょう】
数の大小関係や範囲を表し、その数自身を含み、それを上回る範囲のこと。
例えば、「10以上の自然数」と聞かれたら、「10,11,12,…」のように、10も含めて答える。
不等式で表すときには、≦や≧を使う。 例、$x$は5以上の数 → $x≧5$
一意性【いちいせい】
「ただ1つだけ存在する」という性質。どんな方法を使っても必ず1通りに表せるときに使う用語。
「一意で定まる」や「一意である」、「一意的」といった表現の違いはあるが、意味は同じ。
有名なものは「算術の基本定理」。これは、素因数分解は一意で表せることを示している。
位置関係【いちかんけい】
空間上の2つのもの(直線や平面)の場所がどのようになっているかを表したもの。
「2つの直線」、「2つの平面」、「直線と平面」の3種類がある。
「2つの直線」の位置関係は、「交わる」「平行」「ねじれ」。
「2つの平面」の位置関係は、「交わる」「平行」。
「直線と平面」の位置関係は、「交わる」「平行」「直線が平面上にある」。
特に「ねじれ」は直線の位置関係を表す重要な言葉なので頻出。
一元【いちげん】
未知数が1つであること。主に未知数$ x $という一種類の文字だけが使われていること。
例えば、$ 3x+12=0 $のような式を「一元一次方程式」、$ x^2-3x-10 $ を「一元二次方程式」という。
ただし、「一元」はわざわざ表記しないことが多い。
未知数が2つになると「二元」という言葉を使い、$ x+y=5 $のような式は「二元一次方程式」という。
一次【いちじ】
関数や方程式などの次数が1であること。多項式では二乗以上の未知数が含まれていない状態になる。
「一次関数」、「一次方程式」のように、式の特徴を表す語句としてセットで扱うことが多い。
一次は「文字が1つ」というよりも、「未知数(値が定まっていないもの)が1つ」と考える。
例えば、「 $ax+b=0$ 」は、 $a$ 、$b$ を係数、定数として扱う場合は、一次式である。
$ax$ の項を見ると二次になっているが、$x$ だけが未知数なので、一次式となる。
※「一次式」にも同じ内容を記載
一次関数【いちじかんすう】
$x$ の一次式で表される関数。直線の式で表される。
一般式は$ y=ax+b $であり、$ a $は傾き、$ b $は切片($ y $切片)という。
一次関数の場合、傾きと変化の割合は一致するため、同じものとして考える。
一次元【いちじげん】
次元(座標)が一つだけの空間。「直線上だけの世界」と考える。数直線は一次元である。
時間も過去からずっと一直線につながっているものととらえると一次元である。
$x$ 軸だけなら一次元であるが、$ y $軸が垂直に加わると座標空間ができる。これが二次元である。
一次式【いちじしき】
次数が1の式。式として広くとらえた表現であり、一次関数や一次方程式、一次不等式もすべて一次式である。
一次は「文字が1つ」というよりも、「未知数(値が定まっていないもの)が1つ」と考える。
例えば、「 $ax+b=0$ 」は、 $a$ 、$b$ を係数、定数として扱う場合は、一次式である。
$ax$ の項を見ると二次になっているが、$x$ だけが未知数なので、一次式となる。
※「一次」にも同じ内容を記載
一次不等式【いちじふとうしき】
主に $x$ の一次式で表される不等式を指す。 不等号を用いて、数の大小関係を表す式となっている。
一次方程式と同様の方法で解くことができるが、「両辺に負の数を掛けたり割ったりすると、不等号の向きが変わる」という重要な性質がある。
変数・未知数が2つ以上ある場合(例.$ x+2y>0 $)は、「2桁の整数となるように」などの条件が付加されていることがあるため注意する。
一次変換【いちじへんかん】
行列を用いた、ベクトル空間の写像の一つ。定数項のない一次式に変換されるため、一次変換という。
ある点の座標を別の座標に移す(点を動かす)計算方法と考えると良い。
座標を移す計算方法は様々なやり方があるが、この一次変換では、行列の掛け算によって座標を移す方法となる。
例えば、(3,2)という座標を、原点対称に動かしたいときは、以下の正方行列を使って計算をする。
$$\left(\begin{array}{cc} -1 & 0 \\ 0 & -1 \ \end{array} \right)
\left( \begin{array}{cc} 3 \\ 2 \end{array} \right) =
\left( \begin{array}{cc} -3 \\ -2 \end{array} \right)$$
一次方程式【いちじほうていしき】
一次の多項式で表される方程式。与えられている未知数( $x$ など)の値を求めることが目的となる。
最も基本的な方程式の形であり、あらゆる場面で活用できる。
与えられている未知数が1つだけならば、解はただ1つに求められる。
未知数が2つ以上の場合は、解が1つに定まらない。例えば、$ x+y=3 $は $x=1、y=2$ や $x=3、y=0$ などがある。
そのため、この場合は「連立方程式」として、別の一次方程式も利用して1つの解を求めることになる。
位置ベクトル【いちべくとる】
原点 $O$ を始点としたベクトルのこと。原点を基準にすることで、点の位置(座標)をベクトルとして扱うことができる。
図示する場合では、原点 $O$ は表記しないことが多い。
原点という共通の基準を用いるため、特殊な点の位置(重心、内心、内分点など)を調べる際に有用である。
一般化【いっぱんか】
特定の場合だけでなく、あらゆる場面で利用できるように表すこと。
人間を「動物」と言ったり、火星を「惑星」と言ったりすることも一般化である。
数学においては、法則性を数式で表すことを指す場合が多い。
例えば、三角形の内角の和は「180°」であるが、一般化すると、 $n$ 角形の内角の和は「180°×( $n-2$ )」である。
「三角形」という特定の場合だけではなく「$n$ 角形」として一般化することで、どんな多角形の場合でも数字を当てはめれば内角の和を求めることができるようになる。
一般化するということは、数学の目的の一つでもある。様々なものを数式を使って表すことで、世の中の多くの出来事に応用することが可能となる。
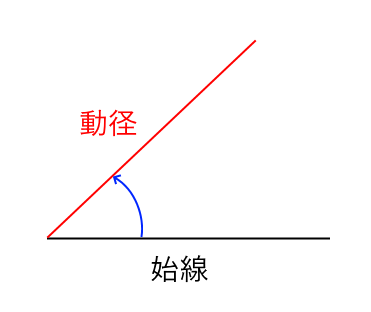
一般角【いっぱんかく】
平面上で、基準となる半直線(始線)から、もう一つの半直線(動径)がどのくらい回転したかを表す角度。
時計の針をイメージするとわかりやすい。反時計回りを正の向き、時計回りを負の向きとする。
0°から360°という制限を無くし、どのような角度でも表現することができる。
一般形【いっぱんけい】
ある数式について、一般化して整理された式の形のこと。括弧が一つもない式で表される。一般式と呼ぶこともある。
例えば、円の一般形は $x^2+y^2+lx+my+n=0$ という式になる。
一方、円の $(x-a)^2+(y-b)^2=r^2$ という式は標準形という。
一般項【いっぱんこう】
数列の第 $n$ 項を $n$ の式で表したもの。$n$ に数字を代入することで、任意の項の値を求めることができる。
数列の特徴によって一般項のパターンは決まっており、主に「等差数列」「等比数列」「階差数列」の3パターンが挙げられるが、他にも「漸化式」を用いて一般項を求める方法がある。
一般式【いっぱんしき】
数学では一般形と同じ意味で用いる。化学において、組成式を意味する用語として使う方が多い。
一般性【いっぱんせい】
すべての場合において当てはめることができる性質のこと。
数学では、「一般性を失わない」という表現で使われる。これは、「特別な場合だけ調べても、すべての場合について調べることと同じ」というときに用いる言葉である。
例えば、「$x+y+z=1$ を満たす3つの異なる整数…」という式のとき、$x$ 、 $y$ 、 $z$ は入れ替えても問題がないため、$x<y<z$ とすることで、当てはまる数値を調べやすくなる。 $x<y<z$ で出てきた結果は、数値を入れ替えることですべての場合を示せるので「一般性を失わない」のである。
対称性のある変数がある場合に、「一般性を失わない」手法は特に有効であるが、自明でない場合は根拠を示さないといけないので注意。
因数【いんすう】
数や整式を積の形で表したときの1つ1つの数や整式のこと。因子とも呼ぶことがある。
例えば、10という数は2×5と表せる。このときの「2」と「5」が因数である。
整式においては、 $x^2+3x+2$ という式は $(x+1)(x+2)$ と表せる。「$x+1$」と「$x+2$」が因数である。
因数定理【いんすうていり】
「整式 $f(x)$ について、 $f(a)=0$ であるとき、$(x-a)$ を因数に持つ」という定理。
3次以上の多項式の因数分解に特に有効で、代入して0になる値を見つけられれば、元の整式から次数を下げて表すことができる。
因数分解【いんすうぶんかい】
数や整式を積の形に直す操作のこと。数や整式をいくつかの因数に分解をする計算。
主に「整数での因数分解(素因数分解)」と「多項式の因数分解」の2つが挙げられる。
より簡単な(小さい)数や整式にできるため、どちらも数学においては非常に重要な計算である。
多項式の因数分解は「展開の逆をたどる計算方法」と考えることができる。
植木算【うえきざん】
一定の幅で木や柱を立てていくとき、本数または幅の長さを求める問題。中学受験で必須となる算数の問題である。
「一直線上にあり、両端にも立てる」
「一直線上にあり、両端には立てない」
「円形に囲むように立てる」
の3パターンの計算方法があるが、中学受験では「石があるところには木は植えない」や「T字型に植える」のように変則的なパターンもある。基本は上記3パターンを応用する。
裏【うら】
命題「 $p \Rightarrow q$ 」に対して、「 $\overline{p} \Rightarrow \overline{q}$ 」のことを裏という。
条件を否定したものであり、「クジラであるならば哺乳類である」に対して、「クジラでないなら哺乳類でない」が裏ということになる。
元の命題と真偽は必ずしも一致しない。
現実でもこれを勘違いして間違った論理展開をしたケースがある。例えば以下の文。
「この本を読んで勉強すればお金持ちになれる。つまり、この本を読まないとお金持ちになれない」
「元の命題が正しい」としても、そこから「裏も正しいとはいえない」ので注意する。
鋭角【えいかく】
0°より大きく、90°より小さい角度。鋭い角度であることを指す。
0°から180°までの角度は「鋭角」「直角」「鈍角」の3つに分類される。
鋭角三角形【えいかくさんかくけい】
3つの角すべてが90°より小さい(鋭角)である三角形のこと。正三角形も含まれる。
どの角度を扱っても、三角比(sin、cos、tan)がすべて正の数になるため、扱いやすい三角形である。
円【えん】
平面図形の一つであり、ある定点から等しい距離にある点の集合である。円形ともいう。
定点のことを「中心」、定点から等距離の点まで長さを「半径」という。
中心の位置と半径の長さが分かれば、コンパスを使って作図ができる。
円に関わる用語は数多く存在(弦、弧、扇形など)し、重要度も高い。
三角形や四角形といった他の平面図形と組み合わされて使用されることもある。

演繹法【えんえきほう】
一般的な前提をもとに、いくつかの情報を段階的に結び付けて結論を出す思考法。
有名な演繹法としては、「三段論法」がある。
「ロシアは寒い」→「モスクワはロシアにある」→「したがって、モスクワは寒い」
数学や理科は基本的にはこの思考方法を用いており、様々な前提や数式を結び付けて結論を導いている。
例えば「三角形の内角の和は180°」という前提を使って、様々な図形問題が解けるのである。
演繹法には弱点があり、それは「前提が間違っている(主観が混じっている)」と破綻してしまうという点。
上記の「ロシアは寒い」という前提が間違っていると、「モスクワは寒い」が成り立たなくなるということである。
もしも数学の様々な前提が間違っていたとすると、世の中の数学を用いたシステムが信用できなくなるということになってしまう。そのために、数学は「正しいと一般に認められたこと」で積み重ねられており、新たな定理が見つかったとしても、本当に正しいのかどうか慎重に調べることになる。
別の思考方法として「帰納法」がある。
円弧【えんこ】
円の円周上の一部分。単に弧ということもあるが、こちらは円ではない曲線も含めて使う場合がある。
角度の「弧度法」は単位円における円弧の長さを表したものである。
演算【えんざん】
計算をすること。一定の法則によって表された式に従って、数値を求めること。
計算と同じ意味で使っても差し支えない。
演算子【えんざんし】
演算を表す記号。数学やプログラミング言語で用いる。
四則(+ー×÷)や等号・不等号(=≠<>≦≧)を始めとする、数式で用いる様々な記号はすべて演算子である。
「計算」だけでなく、「関係性(大小関係など)」や「論理(and、orなど)」を表すために非常に有用である。
円周角【えんしゅうかく】
円周上のある1点から、他の2点に線分を引いたときにできる角。
円周上にある角。
中心角と関係性が深く、主に「円周角の定理」で用いられる角である。
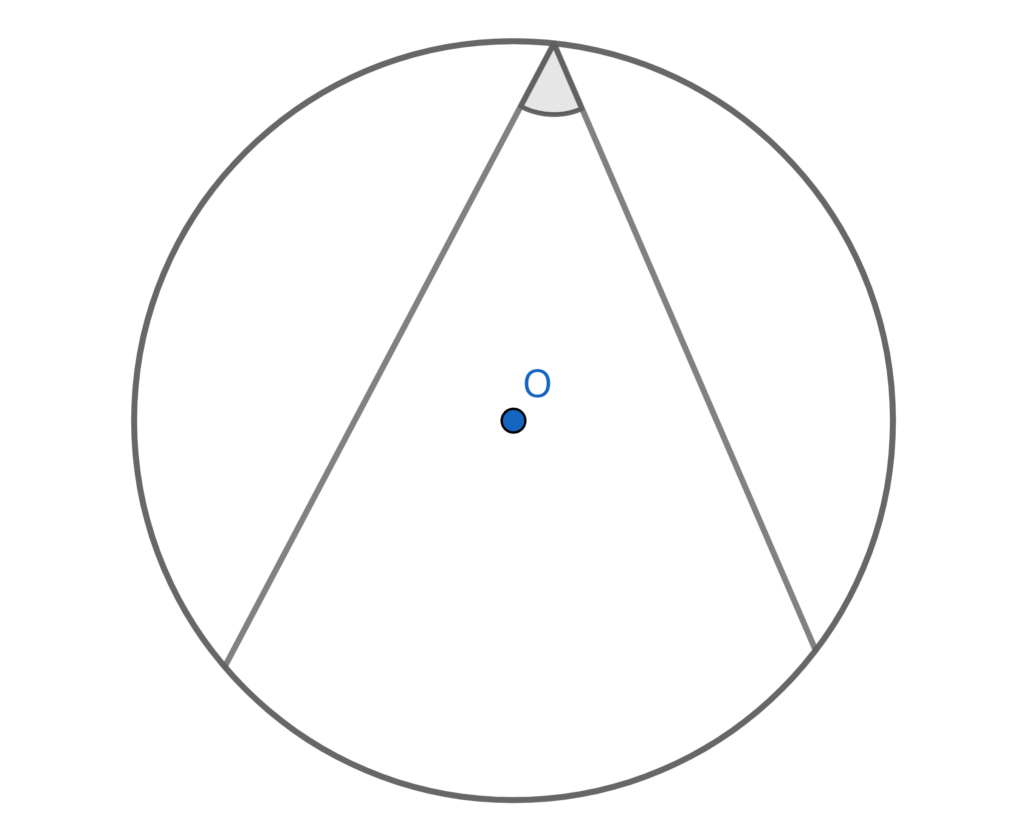
円周角の定理【えんしゅうかくのていり】
「同じ弧に対して、円周角の大きさは等しく、その大きさは中心角半分である」という定理。
円における問題では非常に汎用性が高く、補助線を引いて円周角を作ることで解決の糸口が見つかることも少なくない。
特に、「直径に対する円周角は直角」という性質があり、これは「タレスの定理」という。
「円周角の定理の逆」というものもあり、4点が同一円周上にあることを示すものである。
円周率【えんしゅうりつ】
円の直径に対する長さの比率。ギリシャ文字のπで表される。無理数であり、超越数。
大型コンピュータにより、小数点以下何十兆桁までも判明しているが、数値計算では「3.14」までが主に使われる。
ギネス世界記録では、約7万桁の暗唱が記録されている。
西暦2000年頃、学習指導要領の改訂により「ゆとり教育により、小学校では円周率は3で計算する」ということが話題になった。実際は誤解であり、小数点以下の数値も小学校では教えていたが、教育関係者でも話題にあげる人が多く、大きな議論を呼んだ。
数学における定数としては、様々な計算式に用いられるため、最も重要な定数であるとされる。
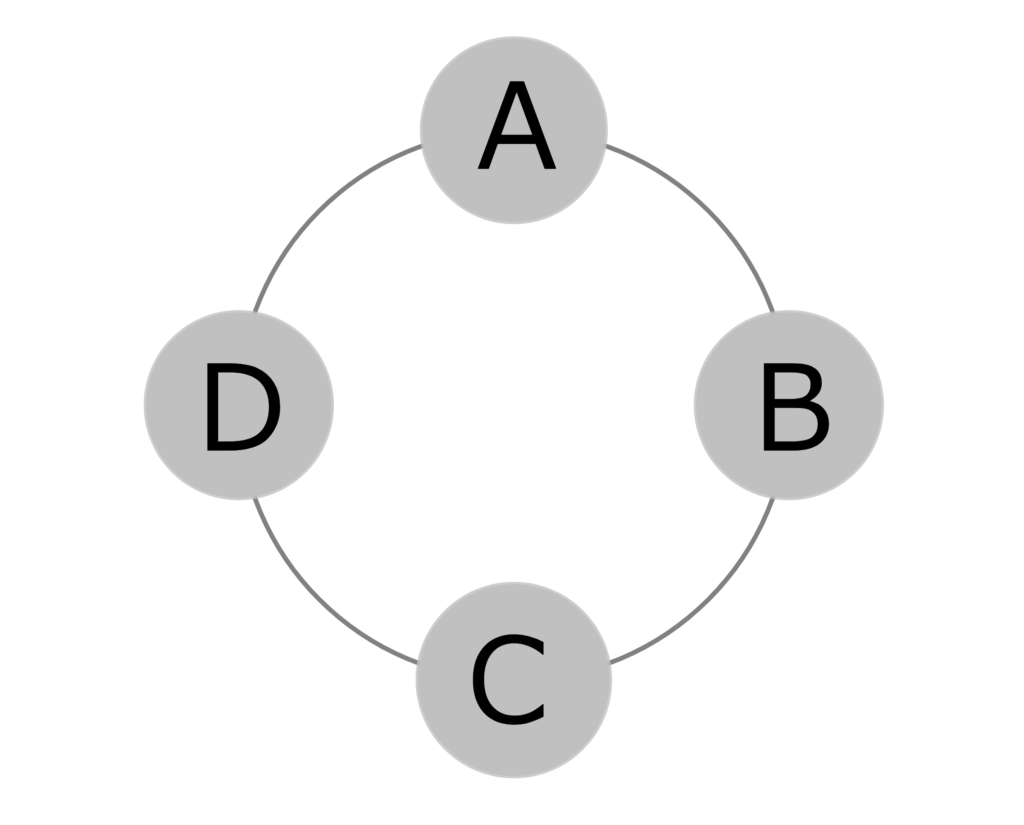
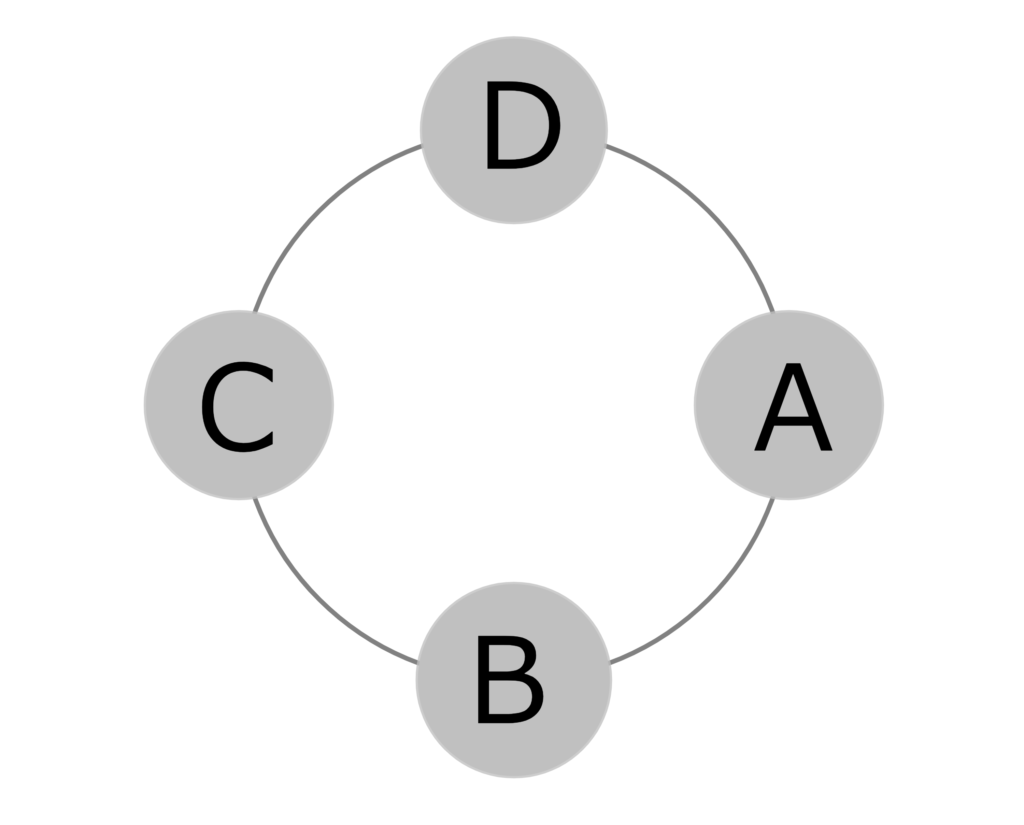
円順列【えんじゅんれつ】
人やものを円形に並べる順列のこと。異なる $n$ 個のものを並べる円順列は $(n-1)!$ で表す。
通常の順列(階乗)と違い、円順列は「見る向きを変えたり、回転させたりすると同じ並びになる」場合がある。
そのため、 $n-1$ のように1を引くことで、同じ並びになる場合を無くしている。
下の図は同じ並びの例である。どちらも時計回りにABCDと並ぶため、同じものと見なす。
似たような順列で「数珠順列」があり、こちらは裏表も考慮する必要がある。
円錐【えんすい】
三次元空間上作られる立体図形の1つで、底面が円の錐体。
英語でcone(コーン)と呼ぶ。
直角三角形の斜辺でない辺を軸にした回転体でもある。
表面は、円と扇形で構成されている。
円錐を切断したときの断面として現れる曲線を「円錐曲線」という。

円錐曲線【えんすいきょくせん】
円錐を切断したときに、断面として現れる曲線のこと。
底面と平行な面で切断すると「円」になるが、切り方を傾けることで、「楕円」、「放物線」、「双曲線」が現れる。
これらは「二次曲線」と呼ばれるものである。
底面から垂直に、軸のすべてを通るように切断すると、三角形の断面になる。これは交差する「2直線」と考える。曲線でないため、円錐曲線に含めない場合が多い。
円積問題【えんせきもんだい】
与えられた円と同じ面積の正方形を作図できるかという問題。作図は定規とコンパスのみを有限回用いる。
結論から言えば、不可能である。
一見すると単純であるため、2000年以上も昔から、多くの数学者が実現可能であると予想し、挑戦した。
この問題は「$π$(円周率)を直線で作図できるか」ということにつながるが、$π$が超越数であるということから不可能であると証明された。
この証明により、逆の「正方形と同じ面積の円の作図」も不可能であることが示されたことになる。
ちなみに、定規やコンパス以外の特殊な道具を用いたり、定規コンパスを無限回用いることを想定したりすれば、作図は可能である。
円柱【えんちゅう】
三次元空間上作られる立体図形の1つで、底面が円の柱体。
英語でcylinder(シリンダー)と呼ぶ。
底面が円の「正円柱」、楕円の「楕円柱」があるが、円柱は「有限の正円柱」を指す場合が多い。
円板【えんばん】
円で囲まれた平面上の領域のこと。円の内部まで含めた図形のことを指す。
円周を含む場合は「閉円板」、円周を含まない場合は「開円板」という。
高校までの範囲では円板と呼ばずに「円」ということが多い。
追いかけ算・追いつき算【おいかけざん・おいつきざん】
2人が離れた位置から同じ方向に進み、後ろにいた人が追いつくまでの時間や距離を求める問題。
算数の問題であり、中学受験頻出の「旅人算」の一つ。旅人算のもう一つは「出会い算」。
距離、速さ、時間の関係を理解した上で、「距離の差」や「速さの差」を考える必要がある。
問題には様々な種類があり、「忘れ物をしたので一度引き返してから追いつく」「校庭のトラックの周りを走り、1周遅れにする」「先に進んていた人が疲れて速度を落とす」など、設定も豊富である。
オイラー【おいらー】
18世紀の数学者、レオンハルト・オイラーのこと。
数学者として後世に与えた影響は非常に大きく、オイラーの名を持つ定理や数式は非常に多い。
オイラーの公式【おいらーのこうしき】
$$e^{iθ}=\cosθ+i\sinθ$$
三角関数と指数関数の関係性を表した式。
起源の異なる三角関数と指数関数であるが、複素数上では密接な関係があることを表している。
この公式により、三角関数と指数関数の書き換えが可能になり、様々な分野に応用ができる。
オイラーの等式【おいらーのとうしき】
$$e^{i\pi}+1=0$$
オイラーの公式のθに $\pi$ を代入して得られる、「最も美しい」とされる等式。
「ネイピア数 $e$」、「虚数単位 $i$」、「円周率 $\pi$」、「1」、「0」という、数学における重要な性質を持つ定数が、上記のような簡単な等式で関係性を表すことができる。
全く別の数学の分野で誕生した 「$e$」、「$i$」、「$\pi$」 を結び付けたこの等式は、多くの数学者に衝撃を与えることになった。
数学者だけでなく、世界中でこの等式に魅了された人も数多くおり、「最も美しい式」との呼び声が高い。
この等式によって、数学的な難問が解決したということはなく、どのように役立つのかは今のところわかっていない。しかし、数学の奥深さが垣間見える等式であることは間違いない。
扇形【おうぎがた】
平面図形の一つであり、円の半径2本と円弧で囲まれた図形である。
扇を広げたような形をしていることから由来する。
基本的には正円のものを指すが、楕円を用いた扇形も存在する。
黄金比【おうごんひ】
$$1:\frac{1+\sqrt{5}}{2}$$
デザインを美しく見せるとされる比。貴金属比の一つ。
絵画や建造物のような芸術作品だけでなく、自然界(特に螺旋構造)にも存在するとされている。
長方形の縦横の比で使われることが多く、ディスプレイやカードなど、完全な黄金比ではないものの、それを意識したつくりにしているものも多い。